テクニカル分析④:Ⅱトレードの勝利を掴む!市場の主要テクニカル分析理論

フラクタル構造
「フラクタル」というのは、「自己相似性」という特殊な性質を有する幾何学的構造のことをいい、図形の全体をいくつかの部分に分解していった時に、全体と同じ形が再現されていく構造である。
自然は一見すると無秩序なカオス状態のようにみえるが、よく観察すると同じ構造が繰り返されている「フラクタル構造」になっている(ものが多く観察される)と言われている。 フラクタル構造を有する図形がフラクタル図形となる。
自己相似性とは、構造の一部が全体の構造と類似していることを指す。
例えば、コーンの先端が小さなコピーのように見えたり、木の枝が全体の形状を反映しているようなものが自己相似性を持っているといえる。
これはフランス人の数学者ブノワ・マンデルブロが考案した概念である。
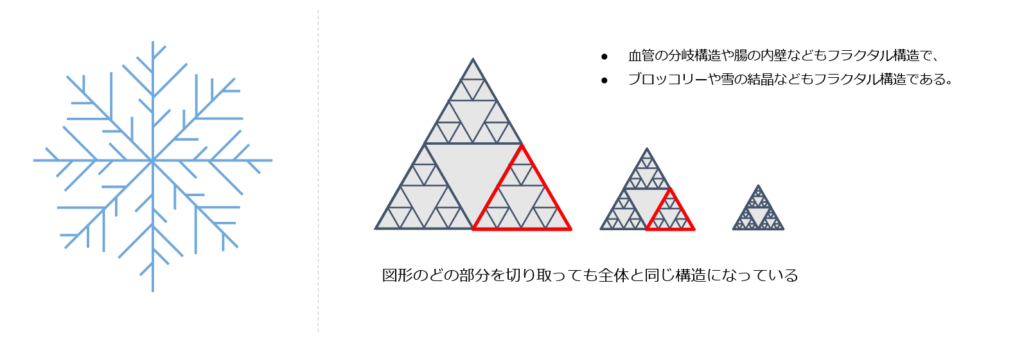
FX(外国為替取引)におけるフラクタル構造は、価格チャート上で見られる特定のパターンを指す。これらのパターンは、自己相似性を示し、相場のトレンドや反転のポイントを示唆することがある。
「日足のなかの4時間足」や「4時間足のなかの1時間足」や「1時間足のなかの15分足」など、時間足を拡大することでフラクタル構造を見つけることができる。
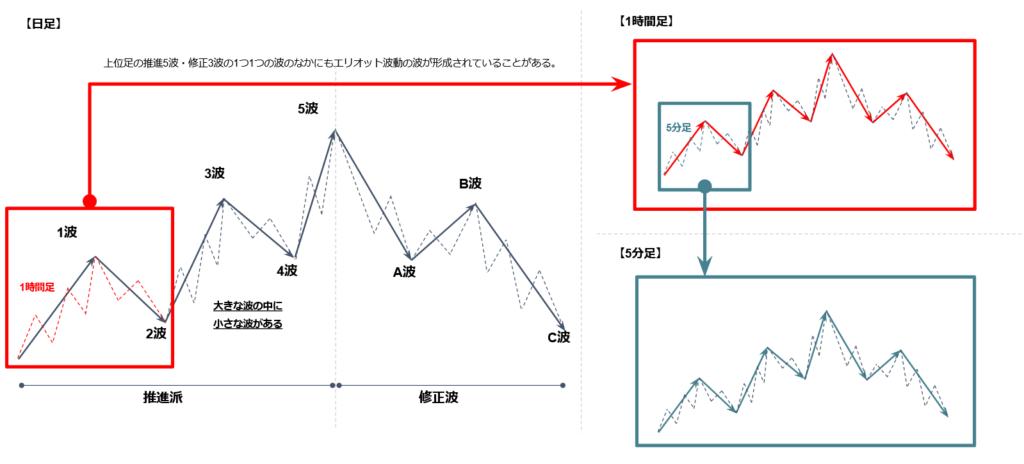
また、[テクニカル分析④:Ⅰ成功する投資戦略!市場の主要テクニカル分析理論]でも解説しているエリオット波動論においても、フラクタル構造が重要な役割を果たしいる。
エリオット波動論では、市場の価格変動が特定の波のパターンで繰り返されると考えられており、これらのパターンはフラクタル的な性質を持っている。
FXにおけるフラクタル構造は、トレーダーやテクニカルアナリストにとって重要な情報源となることがあるため、これらのパターンを理解し、適切に分析することで、市場の動向を予測し、トレードのタイミングを見極める助けとなる。
サイクル理論
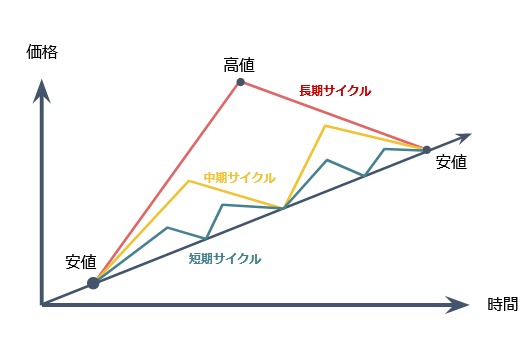
サイクル理論は、経済や金融市場における価格や動向の変化を説明しようとするアプローチの一つである。この理論によれば、市場は一定の周期性を持ち、ある特定のパターンや周期に従って変動するとされる。
この理論では、長期的なサイクルや中期的なサイクル、短期的なサイクルなど、さまざまな周期が考慮される。
サイクル理論の種類
| サイクルの種類 | 期間 | 時間足 | 足の本数 |
|---|---|---|---|
| 長期サイクル | 40-100カ月 | xx | xx |
| 中間サイクル (季節サイクル) | 12-20カ月 | xx | xx |
| プライマリーサイクル | 18-30週 | 週足 | 15-21本前後 (Ave.18) |
| メジャーサイクル (ハーフプライマリーサイクル) | 35-45日 | 日足 | 33-47本前後 (Ave.40) |
| トレーディングサイクル | 10-18日 | xx | xx |
| 4Hサイクル | 5-8日 | 4時間足 | 58~82本前後 (Ave.70) |
| 1Dayサイクル | 1日 | 30分足以下 | 62~83本前後 (Ave.73) |
※各サイクルに対応したローソク足の本数が、期間に記載されている周期とはやや異なっている。この理由は、サイクル理論の生みの親レイモンドA.メリマン氏の著書「相場サイクルの基本:メリマンサイクル論(1995年発売)」で紹介されている周期と、現在の相場周期が異なるからである。
サイクル理論のルール
市場には特定の周期が存在し、これらの周期を特定することが重要である。この周期は、数理的手法や経験則に基づいて見つけることができる。
また、異なる周期が同時に動作することが重要である。つまり、複数のサイクルが同じタイミングで動くことで、市場の変動に影響を与えると考えられている。
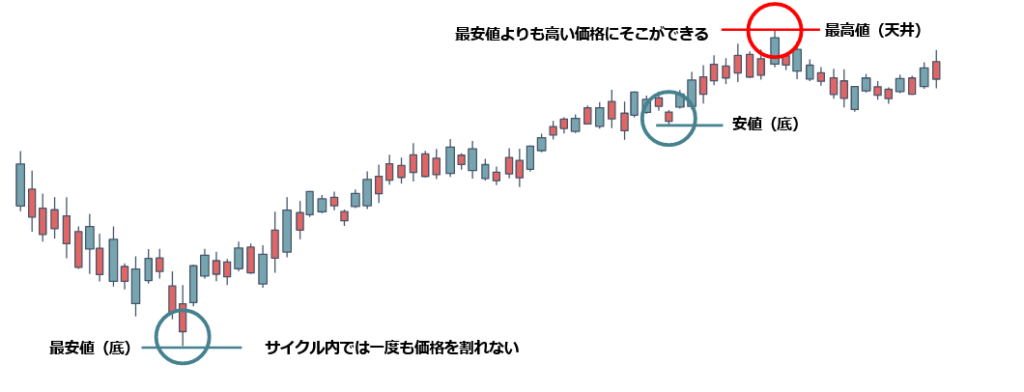
①終点と始点のローソク足は共通
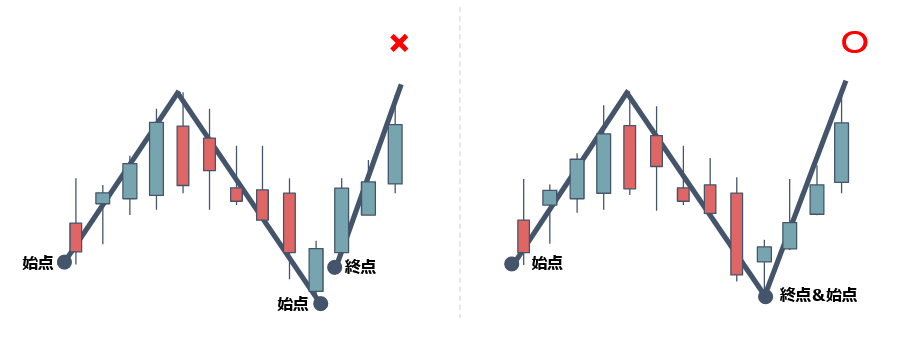
②始点から一番高い所が高値
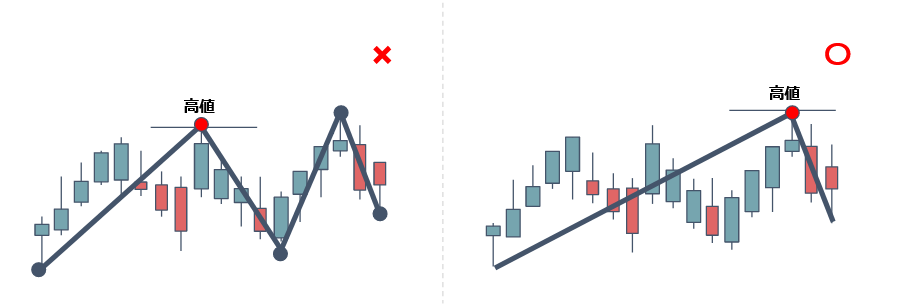
③高値から一番低い所が安値
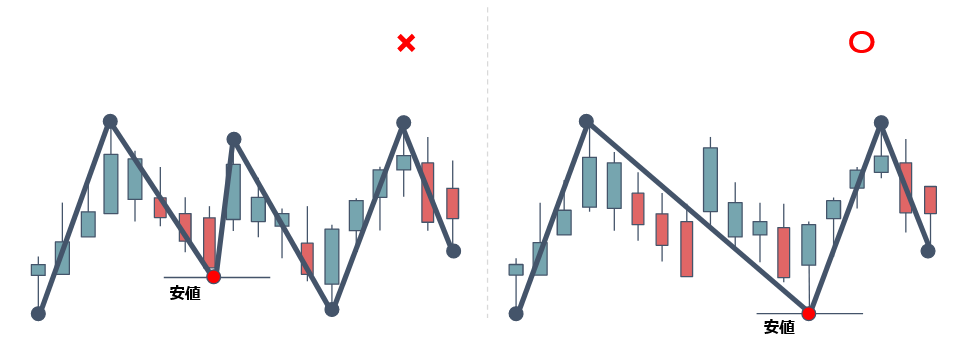
④下位サイクルと上位サイクルの始点と終点は共通
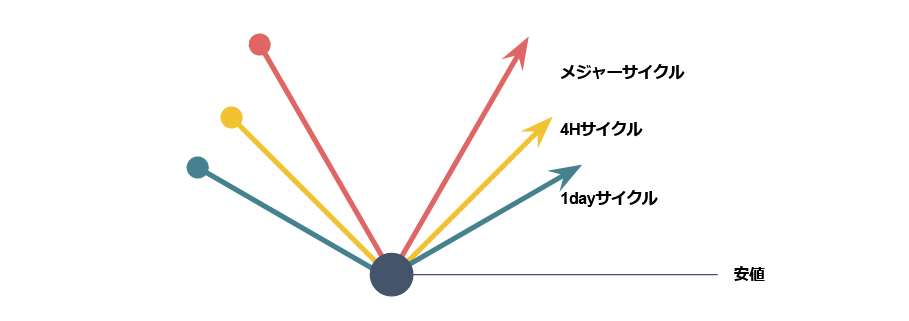
サイクルの型
サイクルの位相の調整が重要であり、サイクルのピークが予測される日付と実際の市場動向との間に生じたずれの調整を行うことで、正確な予測が可能になるとされている。
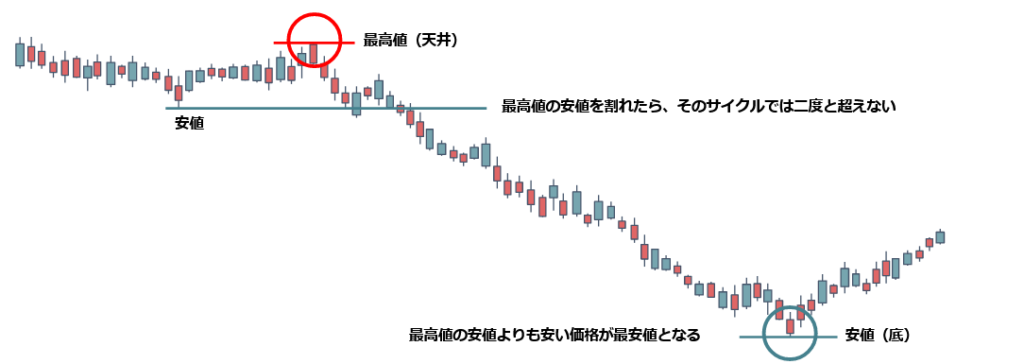
レフトトランスレーション
最初の安値よりも次の安値の方が低い形で終了するサイクル
ライトトランスレーション
最初の安値よりも次の安値の方が高い形で終了するサイクル
オーブ/イレギュラー
オーブ
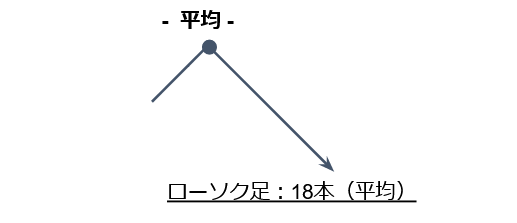
サイクル理論ではサイクルの始まりと終わりを正しく認識した後、その中に含まれるローソク足の数により約8割の割合で再度同様のサイクルが来ることを予測することができる。
ローソク足を数える際の誤差(オーブ)
- オーブ計算式
- 各サイクルのローソク足の平均本数×1/6
- オーブで示された範囲に収まる確率80%
- オーブで示された範囲に収まらない確率20%(イレギュラー)
- 各サイクルのローソク足の平均本数×1/6
- プライマリーサイクルのローソク足の平均本数が18本
- オーブ計算式:18×1/6=±3
- 「±3本」のオーブを考慮すると「15~21本前後」でサイクルが来る可能性が80%であることがわかる。
イレギュラー
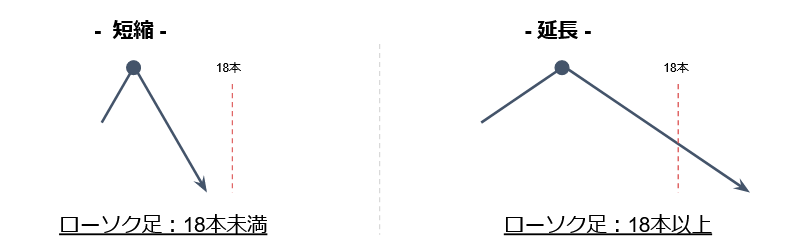
ローソク足がオーブ内に入らない場合は「イレギュラー」となる。
- 短縮:ローソク足がオーブの下限よりも少ない本数で数え終わるイレギュラー
- 延長:ローソク足がオーブの上限よりも多い本数で数え終わるイレギュラー
サイクル理論は、周期的なパターンを用いて将来の市場動向を予測しようとする試みだが、その予測の正確性は常に保証されない。
経済や市場は複雑な要因によって影響を受け、予測が外れることもある。
ただし、サイクル理論は多くの場合において、市場の変動に対する一定の洞察や理解を提供する有用なツールとして利用されている。
値幅観測論(水準論)
値幅観測論(水準論)は直近のチャートから次の上値や下値を予測する方法である。
テクニカル分析の一つであり、価格の変動が一定の値幅や水準に従って観測されるという考え方に基づいている。この考え方によれば、市場は特定の価格水準で支持や抵抗を示し、価格がこの水準を超えるとトレンドが形成されたり、逆転する可能性が高まるとされている。
FXでは、エントリーからイグジットに向けてどれくらいの値幅が変動するかを予測し、トレーダーの戦略に応じて使い分けていく必要がある。下記に値幅を求める計算式を記述する。
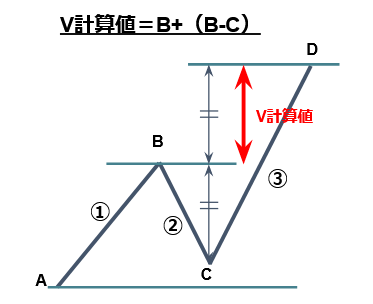
V 計算値
V計算値=B+(B-C)
V計算値は、②の調整の値幅に対し③の値幅は2倍の値幅が出るという計算方法である。①が出た後②の調整が入り、①の高安をブレイクした後の③の値幅が②と同じ値幅と予測される。
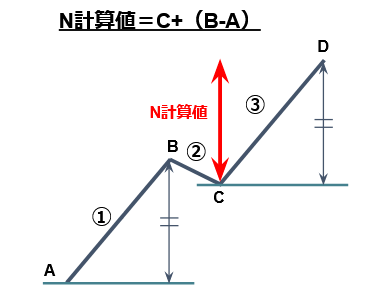
N 計算値
N計算値=C+(B-A)
N計算値は、①の値幅と③の値幅は同じ値幅が出るという計算方法である。①が出た後②の調整が入り、その後①と同じ値幅で③が出ると予測される。
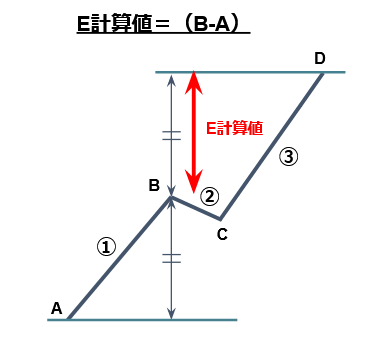
E 計算値
E計算値=(B-A)
E計算値は、①の値幅に対し③の値幅は2倍の値幅が出るという計算方法である。①が出た後②の調整が入り、①の高安をブレイクした後の③の値幅が①と同じ値幅と予測される。
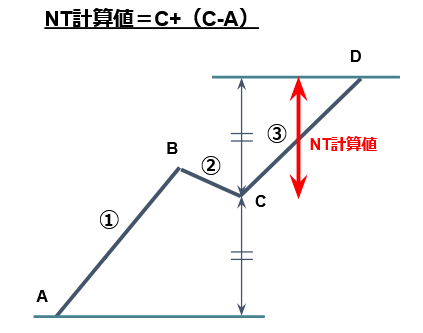
NT 計算値
NT計算値=C+(C-A)
NT計算値は、①の値幅から②の調整の値幅を引いた値幅が③の値幅に出るという計算方法である。①が出た後②の調整が入り、①から②を引いた値幅が③に出ると予測される。
値幅観測論では、価格の水準を基準にして取引のエントリーやイグジットを決定する。
たとえば、価格が特定のサポートラインに近づくと買いポジションを取る、あるいはレジスタンスラインで売りポジションを取るなどのトレード戦略が考えられる。
値幅観測論は、テクニカル分析の中でも重要なアプローチの一つであり、多くのトレーダーや投資家が価格の水準を分析し、取引の判断を行う際の参考にしている。
ランダムウォーク理論
ランダムウォーク理論は、「株価の値動きは常にランダムであり、株価の上昇も下降も同様の可能性で発生する」という理論である。
この理論によれば、市場は情報が完全かつ即座に反映され、それに基づいて価格がランダムに変動するとされている。つまり、将来の価格変動は現在の価格や過去の価格には依存せず、ランダムな要素によって決定されると考えられている。
この理論は、エフゲニー・フィルマンやポール・サミュエルソンなどの経済学者によって提唱された。彼らは、市場参加者が情報を利用して取引を行い、その情報が価格に反映される過程が瞬時に行われるため、価格変動がランダムであるという仮説を立てた。
- 株価は常にランダムで動いており、株価が上がる確率も下がる確率も常に50%
- ランダムウォークは、特定の場面で発現する理論ではなく、常にランダムであるとされています。
- ランダムウォーク理論においては、「株価が上がるのか下がるのかを50%で予測している=ギャンブルを行っている」と考えられることもある。
「猿のダーツ投げ」と「専門家」のポートフォリオに差はない
猿のダーツ投げとは目隠しをした猿がダーツを投げて命中した銘柄で組んだポートフォリオと、株式投資の専門家が組んだポートフォリオの運用成果は変わらないというものである。
株価はランダムに動くため、どの銘柄を選んだとしても似たような結果に辿り着いてしまうという話である。
そのため、株価がランダムに動く以上、専門家がテクニカル分析やファンダメンタルズ分析を駆使して組んだポートフォリオでも、素人が適当に選んだ銘柄のポートフォリオも変わらないという意味でもある。
ランダムウォーク理論は本当に正しいのか
ランダムウォーク理論が正しいのかを考える上で、長年勝ち続けている投資家は正しさを否定する存在となる。
ランダムウォーク理論では、勝率は常に50%であるため、長年株式投資を続けてきた投資家の勝率は、ほぼ50%という説明になってしまうが、実際に勝ち続けている投資家は、50%以上の高い勝率で大きな利益を上げ続けている。
そのため、勝ち続けている投資家がいる以上、ランダムウォーク理論は成立しない理論であると考えることができる。
ランダムウォークは常に正しいわけではない
実際の市場では、ランダムウォーク理論が完全に成立するわけではない。
市場にはさまざまな要因が影響を与えるため、価格変動には一定のパターンやトレンドが見られることがある。ランダムウォーク理論は市場の不確実性やランダム性を強調する一方で、長期的な市場の予測が困難であることを示唆している。
市場も常に情報などの影響を受けて動いているわけではなく、何も情報が無い状態でも動き続ける。買いも売りも優勢でない時に、株価がフラフラと動き続けてランダムウォークとなる。
ランダムウォーク理論が常に正しいわけではないが、市場が方向性を見失った時には、出現するものでもあると考えられる。
ランダムウォークが出現している場面では、勝率は50%となるため勝つことは難しいが、ランダムウォークが出現していない場面では、勝てる可能性が十分ある。そのため、チャートからテクニカル分析で予測をしていくことで、より勝率を上げることが可能になる。
マルチタイムフレーム分析
ルチタイムフレーム分析とは、複数の時間枠で価格チャートを分析し、異なる時間スケールでのトレンドやパターンを考慮して市場を評価する手法である。
通常、トレーダーや投資家は複数の時間枠を同時に使用して市場を分析するが、これにより、より広範囲な視点を得ることができ、より確かなトレードの意思決定が可能となる。
- 上位の時間軸(長期の時間足チャート)を見ながら、下位の時間軸(短期の時間足チャート)でタイミングを取ってエントリーをする。
- 長い時間足のトレンド方向に、その後も進む確率が高いという点に優位性を持たせている。
- 単一の時間のチャートだけでトレードをするよりも、複数の時間チャートを見ることで、視野が広がり、全体を見ながら良いポイントを探せる点にある。
マルチタイムフレーム分析を利用したチャートの読み方
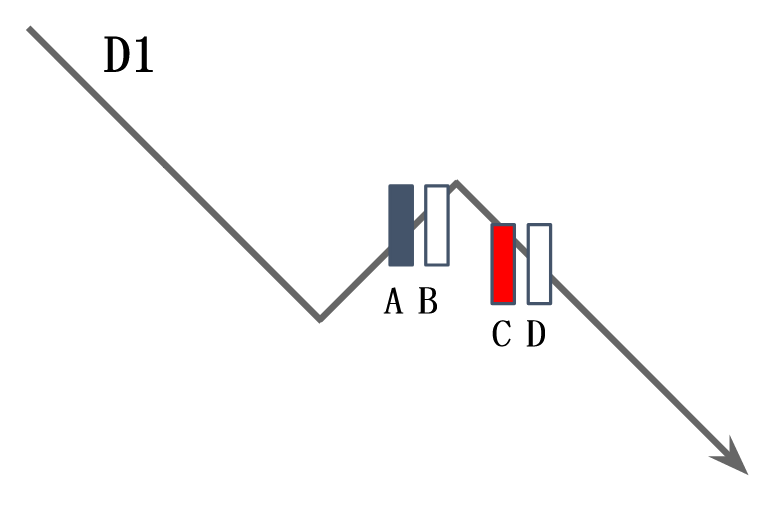
日足(D1)を読む
下記の日足が下降トレンドである場合に、調整部分(A,B)にあるか推進部分(C,D)にあるのを確認する。A-Dのローソク足が大きい場合は以下の1時間足のようにトレンドが出ていることが多い。
またD1がレンジの場合であっても、一本のローソク足が長い場合は、1時間足ではトレンドが出ている場合がある。
下記日足の場合、ローソク足Cが日足の下降トレンド(推進波)かつ、ローソク足が大陰線であることから、最もトレンドが出る可能性が高く値幅も大きく動くと想定される。
※A,Cは大陰線、C,Dは大陽線を示している。Cはわかりやすく赤で色を付けている。
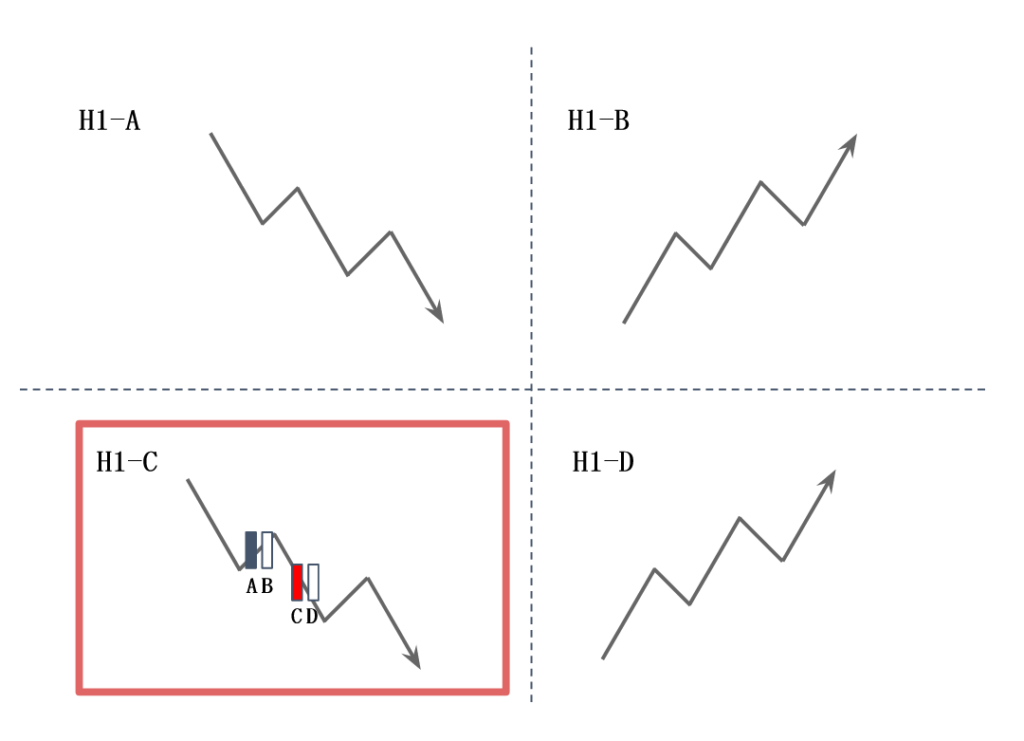
1時間足(H1)を読む
上記日足のA-Dは下記1時間足のA-Dのようにトレンドが出ている場合がある。(日足のローソク足1本分が小さい場合は1時間足ではレンジになっていることが多い。)
上記日足で示したローソク足Cは、下記1時間足のH1-Cのような下降トレンドが出ている可能性が高い。H1-Aも下降トレンドではあるが、日足の調整部分であるため、大きく下げることはないと想定される。
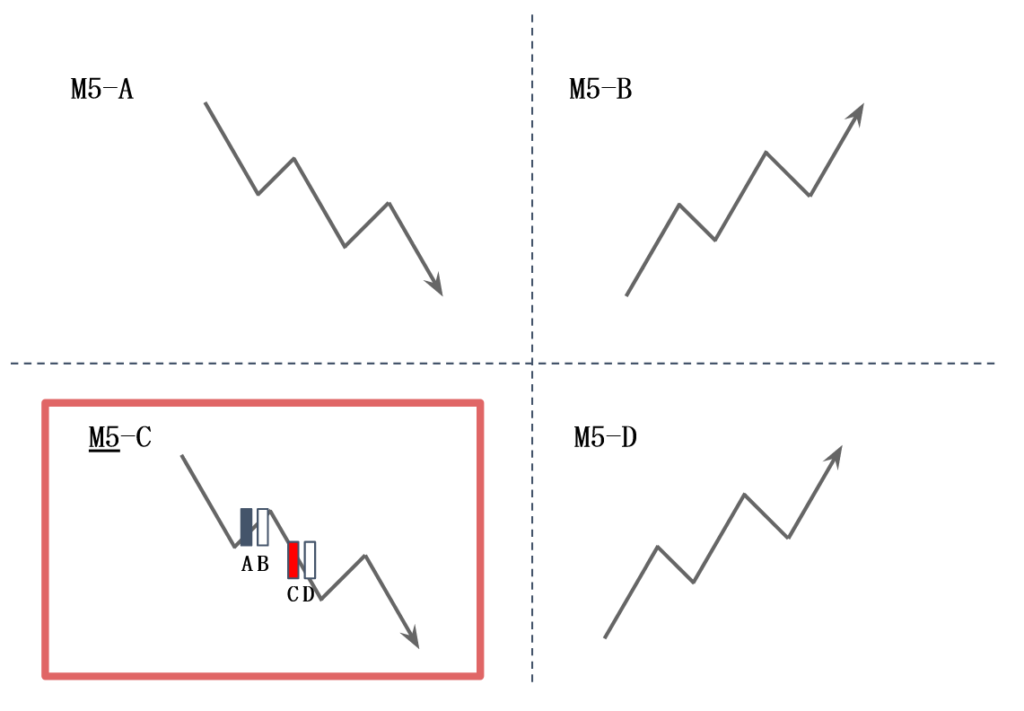
5分足(M5)を読む
続いて、さらにH1-Cに記載されている大陰線Cを見てみると、下記M5-Cのような下降トレンドになっていることが多い。
この時点で、D1,H1,M5のいずれも下降トレンドを示していることから、相場は大きく値幅をつけて下降していることが想像される。
様々な取引の手法があるが、上位足のどの部分に現在日足はあるのか、または1時間足や5分足があるのかを確認することは相場を理解するうえで最も重要ともいえる。
現在トレンドが出ているかを判断するにはダウ理論を学ぶと参考になる場合がある。また、トレンドが推進波か調整波かという判断が必要な場合にはエリオット波動を学ぶとより理解が進む。
一つの理論は複数の理論の上で成り立っている場合が多いため、より広範に理解を進めていくと、相場の世界を深く見ていくことができる。
このブログにある[テクニカル分析④:Ⅰ成功する投資戦略!市場の主要テクニカル分析理論]と併せて学ぶことをお勧めする。
フィボナッチ数列
フィボナッチ数列は、自然界や芸術、経済学、数学などのさまざまな分野で見られる重要な数列である。これらの数は、例えば花弁の数や植物の成長パターン、金融市場の変動など、さまざまな現象に関連している。
また、フィボナッチ数列は、ゴールデンレシオなどの重要な数学的性質とも関連しており、幾何学やアートなどの分野で広く利用されている。
フィボナッチ数列とは
フィボナッチ数列では、最初の2つの数字が0と1であり、その後の各数字は直前の2つの数字を足したものとして生成される。
例えば、最初の2つの数字が0と1なので、次の数字は0 + 1 = 1、次に1 + 1 = 2、その次に1 + 2 = 3、2 + 3 = 5、3 + 5 = 8、と続く。これによって、数列が次々と生成されていく。
- 前の二つの数字を足した数
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610………
イタリアの数学者レオナルド・フィボナッチが1202年のその著書『算盤の書』で、アラビア数字の位取り記数法等のシステムを欧州に導入したことで有名となった。
この著書の中で、兎(うさぎ)の問題により、いわゆる「フィボナッチ数列」の考え方を西洋で初めて紹介したことで、その名を歴史に大きく残すことになった。
兎の問題
1つがいの兎は、生後2か月後から毎月1つがいの兎を産み、兎が死ぬことはないものとする。この場合に、産まれたばかりの1つがいの兎は1年後に何つがいの兎になるか?という問題である。
どの月の合計のつがい数も、その前の2つの月の合計のつがい数の和となり、フィボナッチ数が現れてくる。
| 経過 | 生後0か月 | 生後1か月 | 生後2か月以降 | 合計のつがい数 |
|---|---|---|---|---|
| 0カ月 | 1 | 0 | 0 | 1 |
| 1カ月 | 0 | 1 | 0 | 1 |
| 2カ月 | 1 | 0 | 1 | 2 |
| 3カ月 | 1 | 1 | 1 | 3 |
| 4カ月 | 2 | 1 | 2 | 5 |
| 5カ月 | 3 | 2 | 3 | 8 |
| 6カ月 | 5 | 3 | 5 | 15 |
| 7カ月 | 8 | 5 | 8 | 21 |
| 8カ月 | 13 | 8 | 13 | 34 |
| 9カ月 | 21 | 13 | 21 | 55 |
| 10カ月 | 34 | 21 | 34 | 89 |
| 11カ月 | 55 | 34 | 55 | 144 |
| 12カ月 | 89 | 55 | 89 | 233 |
その他の自然界にあるフィボナッチ数列
- 花弁の枚数
- 百合、アヤメ→3枚
- リンゴ→5枚
- コスモス→8枚
- キク科の植物→13枚,21枚,34枚
- 日本のひまわりの種の並び
- 左回りに21列と右回りに34列
- 左回りに34列と右回りに55列
- 左回りに55列と右回りに89列
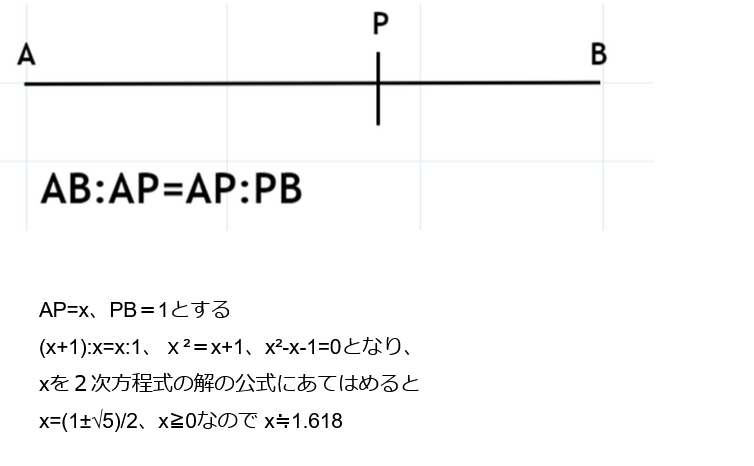
フィボナッチ比率
フィボナッチ比率は、フィボナッチ数列において、連続する2つの数の比率を取ることで得られる数列である。
この比率は、黄金比や黄金分割比とも呼ばれ、一般的には「黄金比率」として知られている。この比率は、フィボナッチ数列の特性に由来しており、様々な自然現象や美術、建築、金融などの分野で広く利用されている。
- フィボナッチ数列を1つ後ろの数で割ると限りなく0.618に近づいていく
- 1,0.5,0.67,0.6, 0.625,0.615,0.619,0.618,0.618, 0.618
- フィボナッチ数列を1つ前の数で割ると限りなく1.618に近づいていく
- 1,2.0,1.5,1.667,1.6,1.625,1.615,1.619,1.618,1.618
- フィボナッチ数列を一つ飛ばした数で割る
- 610÷233=2.618025751
- 233÷610=0.381967213
- フィボナッチ数列を二つ飛ばした数で割る
- 610÷144=4.236111111
- 144÷610=0.236065573
FXにおいて重視すべき数字
0%、23.6%、38.2%、50.0%、61.8%、76.4%、100.0%などのラインがサポートラインやレジスタンスラインになるケースが多いため、投資家から意識されやすいポイントとなる。
これらの数字をフィボナッチリトレースメントやフィボナッチエクスパンションで利用することで、相場の方向や値動きを予測することが可能となる。
- フィボナッチリトレースメント
- 価格チャート上で過去のトレンドの逆行における支持や抵抗のレベルを特定するために使用される。
- この手法では、フィボナッチ数列やその比率(フィボナッチ比率)が価格変動に適用され、トレンドの逆行における重要な価格レベルを見つけるのに役立つ。
- フィボナッチエクスパンション
- 過去の価格の動きを基に将来の価格の可能性を予測するために使用される。
- フィボナッチリトレースメントと同様に、フィボナッチ数列やその比率(フィボナッチ比率)が価格変動に適用されるが、エクスパンションはトレンドの逆行後の価格の可能な方向性や目標レベルを見つけるのに焦点を当てている。
これらの手法は、トレーダーや投資家が市場の動向を予測し、取引の戦略を立てるのに役立つ。
ただし、フィボナッチ数列はあくまで過去の価格動向に基づいて将来の動向を予測するものであり、正確な予測を行うことは難しい場合がある。






